Contoh Soal HOTS Matematika SMP dan Pembahasannya – Hallo sobat pendidik! Memasuki dunia pendidikan revolusi industri 4.0 para guru dituntut untuk mengajarkan materi bermuatan soal HOTS. Terlebih bagi bapak/ibu guru yang mengajar matematika.
Contoh soal HOTS Matematika SMP dan Pembahasannya ini kami sajikan dalam rangka membantu bapak/ibu guru dalam mencari referensi soal HOTS matematika.
Contoh soal HOTS Matematika ini juga dapat dipelajari dengan mudah oleh kalian para peserta didik, karena tentunya telah kami sediakan pembahasannya secara komprehensif. Selamat belajar!
Daftar Isi
Contoh Soal HOTS Matematika SMP dan Pembahasannya
Contoh soal HOTS matematika dan pembahasannya ini tentunya bisa menjadi upaya kita dalam meningkatkan keterampilan berpikir kritis dan berpikir kreatif yang menjadi kebutuhan para peserta didik abad 21.
Telah banyak dibahas melalui seminar dan jurnal ilmiah bahwa salah satu keterampilan yang menjadi tuntutan hidup era digital adalah kemampuan berpikir kritis dan berpikir kreatif.
Kedua keterampilan tersebut dapat dilatih melalui pemberian soal HOTS (High Order Thinking Skills) oleh bapak/ibu guru di sekolah masing-masing selama proses pembelajaran.
Semoga contoh soal HOTS matematika SMP dan pembahasannya yang kami bawakan dapat menambah referensi Anda dalam menyusun instrumen evaluasi, baik itu ulangan harian, PTS maupun PAS.
Selain contooh soal HOTS matematika dalam halaman ini, Anda juga kami anjurkan untuk membuka pembahasan kami selanjutnya, yaitu 20 soal HOTS matematika SMP dan pembahasannya.
Okey, contoh soal HOTS matematika SMP dan pembahasannya yang akan kami sajikan terdiri dari 20 butir soal pilihan ganda. Anda bisa langsung mempelajarinya dengan seksama!
Soal HOTS Materi Garis dan Sudut
Soal no 1~ Contoh Soal HOTS Matematika Mencari Besar Sudut.
Perhatikan gambar berikut!
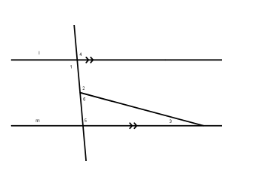
Besar sudut nomor 1 adalah 95°, dan besar sudut nomor 2 adalah 110°. Besar sudut nomor 3 adalah …
A. 5°
B. 15°
C. 25°
D. 35°
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan hubungan dua garis, besar dan jenis sudut, serta sifat sudut yang terbentuk dari dua garis yang dipotong garis lain.
Alternatif cara penyelesaian:
Dari soal diketahui bahwa nomor 1 adalah 95°, dan besar sudut nomor 2 adalah 110°.
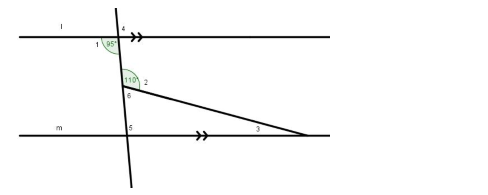
Sudut nomor 4 bertolak belakang dengan sudut nomor 1 sehingga besarnya juga 95°.
Sudut nomor 5 sehadap dengan sudut nomor 4 sehingga besarnya juga 95°.
Sudut nomor 6 adalah pelurus dari sudut nomor 2 sehingga dapat diketahui besarnya 70°.
Sudut nomor 3, 5, dan 6 adalah sudut pembentuk segitiga yang jumlah besar sudutnya 180° sehingga:
sudut nomor 3 + sudut nomor 5 + sudut nomor 6 = 180°
sudut nomor 3 + 95° + 70° = 180°
sudut nomor 3 = 15°
Jadi besar sudut nomor 3 adalah 15°
Soal no 2 ~ Contoh soal HOTS Matematika Menentukan Garis Istimewa Segitiga.
Perhatikan gambar!

Garis RS adalah …
A. Garis berat
B. Garis sumbu
C. Garis tinggi
D. Garis bagi
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan garis-garis istimewa pada segitiga.
Alternatif cara penyelesaian:
Pada gambar di atas garis RS membagi sisi PQ sama besar. Dengan demikian garis merupakan garis berat.
Soal HOTS Materi Lingkaran
Soal no 3 ~ Contoh Soal HOTS Matematika Mencari Luas Juring.
Perhatikan gambar!

P adalah titik pusat lingkaran dan luas juring PLM = 24 cm². Luas juring PKN adalah ….
A. 27 cm²
B. 30 cm²
C. 32 cm²
D. 39 cm²
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan unsur-unsur/bagian-bagian lingkaran atau hubungan dua lingkaran.
Alternatif cara penyelesaian:
Luas juring lingkaran dapat dihitung menggunakan hubungan:
\[\]
$$L juring = \frac{∠ pusat }{360°}×L⊗$$
L⊗= luas lingkaran.
Untuk dapat menghitung luas juring PKN, sebagai “jembatan” dalam hal ini adalah luas lingkaran:
$$L Juring PLM= \frac{∠MPL}{360°}× L ⊗$$
$$24= \frac{45°}{360°}× L ⊗$$
Luas lingkaran = 192
Untuk menghitung luas juring PKN:
$$L juring PKN= \frac{∠KPN}{360°}× L ⊗$$
$$L juring PKN= \frac{60°}{360°}× 192$$
= 32
Jadi luas juring adalah 32 cm²
Soal no 4 ~ Contoh Soal HOTS Matematika Garis Singgung Lingkaran.
Diketahui panjang garis singgung persekutuan luar dua lingkaran dengan pusat P dan Q adalah 15 cm, jarak = 17 cm, dan jari-jari lingkaran = 2 cm. Jika jari-jari lingkaran P kurang dari jari-jari lingkaran Q, maka panjang jari-jari lingkaran Q adalah ….
A. 30 cm
B. 16 cm
C. 10 cm
D. 6 cm
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan unsur-unsur/bagian-bagian lingkaran atau hubungan dua lingkaran.
Alternatif cara penyelesaian:
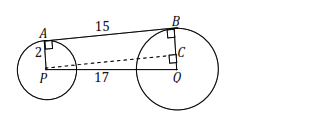
Diketahui:
AB = 15 cm
AP = 2 cm
PQ = 17 cm
PQ < BQ
Akan dihitung panjang BQ.
Dengan bantuan garis PC, diperoleh BC = 2 cm. Perhatikan bahwa AB = PC dan BQ = BC + CQ. Untuk memperoleh panjang BQ terlebih dulu dicari panjang CQ sebagai berikut.
Pada segitiga PCQ berlaku CQ² = PQ²- PC², sehingga:
CQ² = 17² – 15²
= 289 – 225
= 64
Diperoleh CQ = ±8. Karena terkait dengan konteks panjang, maka CQ = −8 tidak digunakan, sehingga CQ = 8.
Sehingga BQ = BC + CQ = 2 + 8 = 10.
Dengan demikian panjang jari-jari lingkaran adalah 10 cm.
Soal HOTS Materi Persamaan Linear
Soal no 5 ~ Contoh Soal HOTS Matematika Menentukan Persamaan Garis.
Persamaan garis melalui titik (2,−3) dan sejajar garis 2x − 3y+ 5 = 0 adalah …
A. 3x + 2y =13
B. 3x − 2y = 13
C. 2x + 3y = 13
D. 2x − 3y = 13
Soal ini menguji kemampuan menentukan gradien, persamaan garis, atau grafiknya.
Alternatif cara penyelesaian:
Persamaan garis 2x− 3y + 5 = 0 terlebih dahulu dinyatakan dalam bentuk eksplisit y = mx +c, sebagai berikut:
2x – 3y + 5 = 0
-3y = -2x -5
y = (2/3) x + 5/3
sehingga sekarang diketahui gradien garis 2x− 3y + 5 = 0 adalah 2/3.
Karena garis yang melalui titik (2, −3) sejajar dengan garis 2x − 3y + 5 = 0 maka gradien kedua garis tersebut sama yaitu 2/3.
Menggunakan rumus persamaan garis melalui titik (x1, y1), yaitu
y – y1 = m(x – x1)
maka:
y – y1 = m(x – x1)
y – (-3) = 2/3(x – 2)
y + 3 = (2/3)x –(4/3)
3y + 9 = 2x -4
2x – 3y = 13
Soal HOTS Materi Kongruensi
Soal no 6 ~ Contoh Soal HOTS Matematika Tentang Kongruensi.
Perhatikan gambar!

Segitiga ABC kongruen dengan segitiga POT . Pasangan sudut yang sama besar adalah ….
A. ∠BAC dan ∠POT
B. ∠BAC dan ∠PTO
C.∠ABC dan ∠POT
D. ∠ABC dan ∠PTO
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan kesebangunan atau kongruensi.
Alternatif cara penyelesaian:
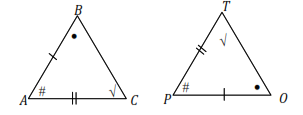 Karena segitiga ABC kongruen dengan segitiga POT maka AB = PO, BC = TO.
Karena segitiga ABC kongruen dengan segitiga POT maka AB = PO, BC = TO.
Dengan demikian ∠BAC = ∠TPO, ∠ABC = ∠POT, ∠BCA = ∠PTO.
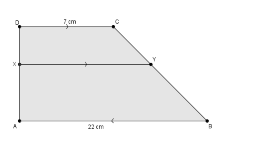
Soal no 7 ~ Contoh Soal HOTS Matematika Tentang Kongruensi.
Perhatikan gambar! Jika CY:YB = 2: 3, maka panjang XY adalah …
 A. 9,0 cm
A. 9,0 cm
B. 11,5 cm
C. 13,0 cm
D. 14,5 cm
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan kesebangunan atau kongruensi.
Alternatif cara penyelesaian:

Dari gambar dapat diketahui bahwa ∆DAE sebangun dengan ∆DXH sehingga:
$$\frac{XH}{AE}=\frac{DH}{DE}$$
$$\frac{XH}{15}=\frac{2}{DH+HE}$$
$$\frac{XH}{15}=\frac{2}{5}$$
$$XH=\frac{2}{5}×15$$
XH = 6
Sehingga panjang XY = XH + HY ⇔ XY = 6 + 7 ⇔ XY = 13
Jadi panjang XY adalah 13,0 cm.
Soal no 8 ~ Contoh Soal HOTS Matematika Tentang Perbandingan.
Sebuah tongkat panjangnya 2 m mempunyai panjang bayangan 75 cm. Pada saat yang sama panjang bayangan sebuah menara TV 15 m. Tinggi menara TV tersebut adalah …
A. 40 m
B. 45 m
C. 48 m
D. 60 m
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan perbandingan.
Alternatif cara penyelesaian:
Persoalan di atas merupakan persoalan perbandingan senilai.
| Ukuran sebenarnya | Panjang bayangan | |
| Tongkat | 2 m | 75 cm = 0,75 m |
| Menara TV | a | 15 m |
dari tabel diatas diperoleh perhitungan:
a = (15/0,75) x 2 = 40, jadi tinggi menara TV adalah 40 cm.
Soal HOTS Materi Bagun Ruang
Soal no 9 ~ Contoh Soal HOTS Matematika Unsur-unsur Kerucut.
Perhatikan gambar kerucut! Garis PQ adalah ….
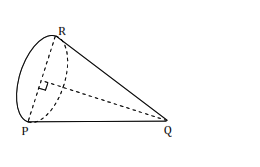 A. jari-jari
A. jari-jari
B. diameter
C. garis pelukis
D. garis tinggi
Soal ini menguji kemampuan menentukan unsur-unsur pada bangun ruang.
Alternatif cara penyelesaian:
Berdasarkan unsur-unsur kerucut, PQ adalah garis pelukis.
Soal no 10 ~ Contoh Soal HOTS Matematika jaring-jaring Bangun Ruang.
Perhatikan gambar di bawah!
 Yang merupakan jaring-jaring balok adalah …
Yang merupakan jaring-jaring balok adalah …
A. I dan II
B. II dan III
C. III dan IV
D. I dan IV
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan kerangka atau jaring-jaring bangun ruang.
Alternatif cara penyelesaian:
Dari keempat gambar di atas jika dilipat sesuai garis maka yang membentuk balok adalah (I) dan (IV).
Soal no 11 ~ Contoh Soal HOTS Matematika Volume Kerucut.
Volume kerucut yang panjang diameter alasnya 10 cm dan tinggi 18 cm adalah …( π = 3,14)
A. 413,0 cm³
B. 942,0 cm³
C. 706,5 cm³
D. 471,0 cm³
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan volume bangun ruang.
Alternatif cara penyelesaian:
Diketahui diameter alas 10 cm sehingga jari-jarinya (1/2) × 10 cm yaitu 5 cm.
Volume kerucut = (1/3) × π × r × r × t = (1/3) × (3,14) × 5 × 5 × 18 = 471. Sehingga volume kerucut tersebut adalah 471,0 cm³
Soal no 12 ~ Contoh Soal HOTS Matematika Volume Bola.
Volume bola terbesar yang dapat dimasukkan ke dalam dus berbentuk kubus dengan panjang rusuk 18 cm adalah …
A. 1296π cm³
B. 972π cm³
C. 468π cm³
D. 324π cm³
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan volume bangun ruang.
Alternatif cara penyelesaian:
Diketahui panjang rusuk kubus adalah 18 cm.
Volume bola terbesar diperoleh jika bola bersinggungan dengan keenam sisi kubus.
Dalam kondisi seperti itu perhatikan bahwa rusuk kubus sama dengan diameter balok, sehingga jari-jari (r) adalah 18/2 = 9 cm.
Diperoleh volume bola = (4/3) π × r³ = (4/3) π x 9 x 9 x 9 = 972π cm³
Soal no 13 ~ Contoh Soal HOTS Matematika Mencari Luas Permukaan Balok dan Limas.
Perhatikan bangun berikut yang terdiri dari balok dan limas! Diketahui balok berukuran 6 cm × 6 cm × 12 cm. Jika tinggi limas 4 cm, luas permukaan bangun adalah …

A. 368 cm²
B. 384 cm²
C. 438 cm²
D. 440 cm²
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan luas permukaan bangun ruang.
Alternatif cara penyelesaian:
Akan dicari tinggi segitiga pada selimut limas;
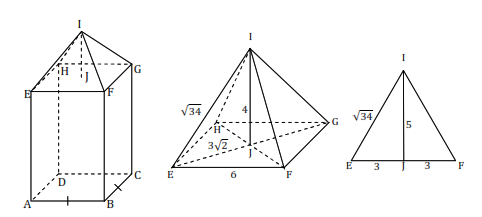
Luas bangun = Luas selimut balok + Luas alas balok + Luas selimut limas
=4 × LABFE + LABCD + 4 × LEFI
=4 × (6 ×12) + (6 × 6) + 4× [(1/2) × 6 × 5]
= (4 × 72) + 36 + (4 × 15)
= 288 + 36 + 60
= 384
Jadi luas permukaan bangun tersebut adalah 384cm²
Soal no 14 ~ Contoh Soal HOTS Matematika Mencari Luas Permukaan Tabung.
Pada gambar di bawah adalah bola di dalam tabung. Jika jari-jari 7 cm, maka luas seluruh permukaan tabung adalah …
A. 343 cm²
B. 294 cm²
C. 147 cm²
D. 49 cm²
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan luas permukaan bangun ruang.
Alternatif cara penyelesaian:
Diketahui bahwa jari-jari bola 7 cm.
Perhatikan bahwa diameter dan tinggi tabung sama dengan diameter bola. Dengan demikian jari-jari tabung (r) = 7 cm, tinggi (t)= 14 cm.
Luas permukaan tabung = 2πr² + 2πr t
= 2π ×7 × 7 + 2π × 7 × 14
= 98π + 196π
= 294
Contoh Soal HOTS Materi Pemusatan Data
Soal no 15 ~ Contoh Soal HOTS Matematika Mencari Modus.
Data nilai ulangan matematika beberapa siswa sebagai berikut: 64, 67, 55, 71, 62, 67, 71, 67, 55. Modus dari data tersebut adalah ….
A. 62
B. 64
C. 67
D. 71
Soal ini menguji kemampuan siswa dalam menentukan ukuran pemusatan yaitu modus.
Alternatif cara penyelesaian:
Modus adalah nilai dari data yang mempunyai frekuensi tertinggi atau nilai dari data yang sering muncul. Modus dilambangkan dengan Mo.
Dari soal yang ada untuk nilai 55 muncul dua kali, nilai 62 dan 64 muncul sekali, nilai 67 muncul tiga kali dan nilai 71 muncul dua kali. Jadi modus dari data nilai ulangan matematika dari soal yang ada adalah 67.
Atau dapat juga dibuat tabel frekuensi terlebih dahulu seperti berikut ini.
|
Nilai Ulangan Matematika |
Frekuensi |
| 55 | 2 |
| 62 | 1 |
| 64 | 1 |
| 67 | 3 |
| 71 | 1 |
| Jumlah | 0 |
Kemudian dicari nilai ulangan matematika yang frekuensinya tertinggi. Dari tabel frekuensi diperoleh bahwa nilai 67 mempunyai frekuensi tertinggi yaitu 3. Jadi modus dari soal yang ada adalah 67.
Soal no 16 ~ Contoh Soal HOTS Matematika Mencari Means.
Dalam suatu kelas nilai rata-rata ulangan matematika 18 orang siswa putri 72. Sedangkan nilai rata-rata siswa putra 69. Jika jumlah siswa di kelas tersebut 30, maka nilai rata-rata ulangan matematika di kelas tersebut adalah ….
A. 68,2
B. 70,8
C. 71,2
D. 73,2
Soal ini menguji kemampuan siswa dalam menentukan ukuran pemusatan yaitu mean atau rata-rata.
Alternatif cara penyelesaian:
Dari soal diketahui bahwa banyak siswa putri ada 18.
Rata-rata nilai ulangan matematika siswa putri 72.
Rata-rata nilai ulangan matematika siswa putra 69.
Banyak siswa satu kelas 30, jadi banyak siswa putra ada 30 – 18 = 12.
Dengan menggunakan rumus rata-rata.
$$\bar{x}=\frac{x_{1}+x_{2}+x_{3}+…x_{n}}{n}$$
maka dapat diperoleh bahwa rata-rata nilai ulangan matematika dari 30 siswa adalah;
$$\frac{(18 × 72) + (12× 69)}{30}=\frac{2124}{30}= 70,8$$
Soal no 17 ~ Contoh Soal HOTS Matematika Bentuk Tabel Frekuensi.
Data usia anggota klub sepakbola remaja disajikan pada tabel berikut.
| Usia (tahun) | 13 | 14 | 15 | 16 | 17 | 18 |
| Frekuensi | 2 | 1 | 6 | 9 | 5 | 3 |
Banyak anggota klub yang usianya kurang dari 17 tahun adalah …
A. 9 orang
B 16 orang
C. 18 orang
D. 23 orang
Soal ini menguji kemampuan siswa untuk menafsirkan data yang disajikan dalam bentuk tabel frekuensi.
Alternatif cara penyelesaian:
Dalam soal ditanyakan banyak anggota klub yang usianya kurang dari 17 tahun berarti jumlah dari banyak anggota klub usia 13, 14, 15, dan 16 tahun.
Jadi banyak anggota klub yang usianya kurang dari 17 tahun ada 2 + 1 + 6 + 9 = 18 orang.
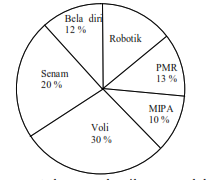
Soal no 18 ~ Contoh Soal HOTS Matematika Diagram Lingkaran.
Diagram lingkaran berikut menunjukkan kegemaran 200 siswa dalam mengikuti kegiatan ekstrakurikuler di suatu sekolah. Banyak siswa yang gemar robotik adalah …
A. 10 orang
B. 15 orang
C. 25 orang
D. 30 orang
Soal ini menguji kemampuan siswa untuk menyelesaikan masalah yang berkaitan dengan penyajian data dalam bentuk diagram lingkaran.
Alternatif cara penyelesaian:
Dari soal diketahui bahwa banyak siswa seluruhnya adalah 200 siswa. Untuk yang gemar bela diri ada 12%, yang gemar senam 20%, yang gemar Voli 30%, yang gemar PMR ada 13% sedangkan yang gemar MIPA 13%.
Persentase siswa yang gemar robotik adalah 100% 12% 20% 30% 13% 10% = 15%
Banyak siswa yang gemar robotik adalah 15 % 200 = 30 siswa.
Contoh Soal HOTS Materi Peluang
Soal no 19 ~ Contoh Soal HOTS Matematika Mencari Peluang Dadu.
Sebuah dadu dilambungkan satu kali. Peluang muncul mata dadu lebih dari 4 adalah….
A. 1/6
B. 1/4
C. 1/3
D. 2/3
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan peluang suatu kejadian.
Alternatif cara penyelesaian:
Untuk menyelesaikan soal nomor 39 ini, siswa harus memahami tentang menentukan peluang dengan setiap titik sampel mempunyai kesempatan yang sama untuk terjadi yaitu dengan rumus:
$$P(A)=\frac{n(a)}{n(s)}, A\subset S$$
P(A) adalah peluang kejadian A
n(a) adalah banyaknya titik sampel dalam kejadian A
n(S) banyaknya seluruh titik sampel
Dari soal diketahui bahwa sebuah dadu dilambungkan satu kali maka hasil pelambungan sebuah dadu sebanyak satu kali adalah muncul muka dadu bernomor 1, 2, 3, 4, 5, 6 sehingga ruang sampelnya adalah S = {1, 2, 3, 4, 5, 6} maka banyak anggota ruang sampel atau n(S) = 6.
Dari soal ditanyakan peluang dari suatu kejadian muncul mata dadu lebih dari 4. Misal A adalah kejadian muncul mata dadu lebih dari 4 maka A= { 5, 6 } dan n(A) = 2. Dengan menggunakan rumus menentukan peluang suatu kejadian A yaitu;
$$P(A)=\frac{n(a)}{n(s)}=\frac{2}{6}\frac{1}{3}$$
Jadi peluang muncul mata dadu lebih dari 4 adalah 1/3
Soal no 20 ~ Contoh Soal HOTS Matematika Menentukan Peluang.
Dalam sebuah kotak terdapat 4 bola kuning, 14 bola merah, dan 6 bola hijau. Sebuah bola diambil secara acak, maka peluang terambil bola berwarna kuning adalah …
A. 1/14
B. 1/6
C. 1/5
D. 1/4
Soal ini menguji kemampuan menyelesaikan masalah yang berkaitan dengan peluang suatu kejadian.
Alternatif cara penyelesaian:
Untuk menyelesaikan soal nomor 20 ini, siswa harus memahami tentang cara menentukan peluang dengan setiap titik sampel mempunyai kesempatan yang sama untuk terjadi, yaitu dengan rumus;
$$P(A)=\frac{n(a)}{n(s)}, A\subset S$$
Dari soal diketahui bahwa dalam kotak terdapat 4 bola kuning, 14 bola merah, dan 6 bola hijau. Banyak bola dalam kotak ada 24 bola sehingga banyak anggota dalam ruang sampel adalah n (S ) = 24.
Selanjutnya karena sebuah bola diambil secara acak dari kotak tersebut berarti setiap bola mempunyai kesempatan yang sama untuk terambil. Dari soal ditanyakan peluang dari suatu kejadian terambil bola berwarna kuning.
Misal A adalah kejadian terambil bola berwarna kuning maka banyak kemungkinan terambilnya bola berwarna kuning ada 4 kemungkinan karena bola kuning ada sebanyak 4 buah maka n(A) = 4.
Dengan menggunakan rumus menentukan peluang suatu kejadian A yaitu:
$$P(A)=\frac{n(a)}{n(s)}=\frac{4}{24}\frac{1}{6}$$
Jadi peluang terambil bola berwarna kuning adalah 1/6.
Demikian contoh soal HOTS matematika SMP yang dapat kami ulas pada kesempatan kali ini. Semoga 20 nomor contoh soal HOTS matematika sekaligus dan pembahasannya dapat menambah referensi para pembaca budiman.
Contoh soal HOTS matematika jenjang SMP maupun untuk jenjang yang lain bisa anda akses pada artikel kami yang lain. Salam Pembelajar!








1 comment